Dans ma classe de cycle 2, nous avons un créneau de mathématiques tous les matins.

La classe est séparée en 2 groupes :

                        La première moitié de classe est installée au coin regroupement avec moi pour travailler sur des créations Mathématiques.
Les élèves ont eu un court temps auparavant pour préparer une création sur leur petit carnet.
Les élèves du jour apportent leur carnet au coin regroupement.

Je recopie sur une feuille A3 leur création puis m'assois avec eux.
Les élèves prennent tour à tour la parole pour lire, commenter, corriger ou ajouter des choses.
Ils se lèvent si besoin pour venir écrire sur la création en couleur.

Quand ils considèrent avoir fait le tour, on passe à la création Maths suivante.

 

Ce temps permet une réelle discussion mathématique. Les enfants s'approprient les concepts mathématiques et progressent ensemble.
Ils me demandent de l'aide quand ils ont besoin. Je suis garante du respect des règles de parole mais je fais aussi attention à ce que le contenu mathématique soit juste.
Je n'hésite pas à poser des questions pour relancer le débat.

______________________

         Pendant ce temps, l'autre moitié de la classe est en travail individuel. Les élèves disposent d'un plan de travail qui leur rappelle les activités dans lesquelles ils peuvent s'investir pendant cette séance. Ils travaillent en autonomie.

Je les surveille du coin de l'oeil afin de faire respecter un niveau sonore propice au travail de chacun et afin de m'assurer que chacun ait les moyens de travailler.

 

 

 

 Sur les tables, à plusieurs, des élèves réalisent des fiches de Numérations-Opérations sur leur cahier du jour.

 

 

 

 

 

Dans un coin de la salle, deux élèves apprennent à compter avec les clés de laçages additions.

 

 

 

 

Par terre, quatre élèves se sont mis ensemble pour travailler avec le matériel de manipulation.

Voici leur production : 

 

A côté, deux élèves découvrent les égalités avec la balance mathématiques.

"Si on met pareil de chaque côté, la balance est à plat."

 

 

 

 D'autres, sur les tables, progressent dans leur cahier de calcul.

 

    A la fin de chaque séance, les enfants peuvent présenter ce qu'ils ont appris et leurs difficultés à la classe.

 Le lendemain, toute la classe complète la fiche "exercices" récapitulative des créations mathématiques dans son cahier du jour et c'est reparti ;).

 

 

Tout le monde travaille et apprend à son rythme =) .

Bonjour à tous et bienvenue sur notre blog!

N'hésitez pas à vagabonder sur celui-ci pour découvrir nos pratiques de classe, nos réflexions, nos actualités...

Au cours de ma première année en C. P., j’ai enseigné la lecture avec une méthode de lecture syllabique assez stricte, c’est à dire que la part du décodage était très importante. Mes élèves ont donc appris à lire comme on déchiffre une partition. J’étais conquise ! Les résultats ont été rapides, les élèves « lisaient » de plus en plus vite, de plus en plus de sons. J’ai donc passé mon année, comblée, à enchaîner les phonèmes dans une routine sécurisante.

 

Le réveil a été brutal, lorsque j’ai retrouvé ces mêmes élèves au C. E. 1 avec de nouvelles attentes : compréhension, étude de la langue, production d’écrits… La catastrophe.

 

De nombreux élèves n’arrivaient pas à entrer dans l’orthographe, ni la grammaire, ni la conjugaison. Je leur avais martelé, pendant un an que l’écriture était faite de sons. Pour eux, « gè » et « j’ai » étaient la même chose. Impossible pour eux de saisir la différence. Pourquoi ajouter, à la fin d’un mot, un S qui ne s’entend pas ?

 

« Gè troi cha », m’écrivaient-ils avec fierté. En comment leur en vouloir, puisqu’en CP je leur demandais d’écrire la syllabe « cha » et me satisfaisait du résultat.

 

En compréhension, le constat était aussi atterrant. Les élèves lisaient rapidement, sans se soucier du sens. La plupart étaient capables de comprendre ce qu’ils lisaient mais, ils ne cherchaient pas à le faire. Les yeux parcouraient les phrases, les sons sortaient, c’est tout ce que je leur avais demandé jusqu’à présent. Tous les adultes autour étaient satisfaits de cette compétence en « solfège ». Je leur avais « caché » le véritable objectif de la lecture puisqu’à aucun moment je ne l’avais réellement mis en évidence.

 

Je me suis donc acharnée, pendant cette année de C. E. 1, à corriger mes erreurs et à donner de nouvelles habitudes à mes élèves. Il est évident que cela à été long et pénible, pour moi comme pour eux et que cette méthode, même si on a l’impression que les élèves progressent vite, n’est pas la plus efficace…

Tous les jours, les nouveaux C. P. écrivent des textes dans leur cahier jaune. Sur une double page, ils font un dessin (côté blanc) et une histoire (côté seyes).

 

Mes C. P. commencent souvent par le dessin. Je passe les voir pour les aider à écrire leur texte. Pour le premier texte, j’écris quasiment tout en dictée à l’adulte. Petit à petit, je laisse des trous dans le texte pour qu’ils écrivent seuls les mots qu’ils connaissent ou qu’ils peuvent trouver facilement. Rapidement, ils se sont mis à écrire tout seul et à venir me demander quelques mots.

 

Chaque semaine, un texte est choisi pour servir de référent : il est affiché dans la classe et collé dans le cahier de vie.

 

Le premier de l’année était : Le chevalier est gentil.

 

Pour s’approprier le texte, on le travaille collectivement :

 

- On le récite en pointant les mots.

- Je demande aux élèves de me montrer le mot « chevalier ».

- « Quel est ce mot ? »

- « Écrivez sur votre ardoise le mot « est » ».

- Je fais varier le texte avec les mots qu’ils connaissent déjà, par exemple ici, les mots de la classe :

« Noé est gentil. », « Nathan est gentil. »… Ce qui permet, dans la foulée, de remarquer que « gentil » est masculin et que, pour une fille, on dit « gentille ».

- Je donne à chaque élève les étiquettes de chaque mot.

- Je prépare des exercices de réinvestissement ...

 

Un texte libre par semaine est choisi par les élèves pour « le toilettage » : lecture, analyse, modification...

 

En ce tout début de C. P., deux textes libres nous servent de textes référents :

 

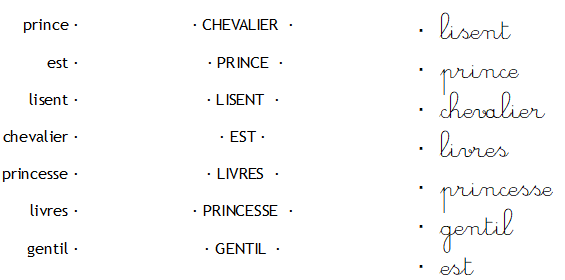
« Le chevalier est gentil. »

 

« Le prince et la princesse lisent des livres. »

 

 Après avoir travaillé collectivement ces textes, les élèves ont des exercices à faire en autonomie, sur le cahier du jour. En voici quelques exemples:

 

• Savoir reconnaître les mots dans les trois graphies :

• 

• Transcrire d'une graphie à l'autre

• 

• Retrouver les mots dans les textes.

• 

• Lire des mots (et dessiner à côté)

• 

• Lire de nouvelles phrases (et coller la bonne image)

• 

• Produire de nouvelles phrases avec les étiquettes des mots des textes et les prénoms de la classe.

• Recopier le texte à partir d'un modèle en cursive ou en script...